Was analog geschieht, kann mit sehr viel weniger Platzaufwand heute auch digital erreicht werden. Das ist auch der Grund, warum die Geräte heute immer kleiner und auch (un)handlicher werden.
Um zu verstehen, wie eine digitale Signalverarbeitung funktioniert, muß man zunächst einmal wissen, daß dazu ein Computer oder integrierte Bausteine, sog. IC´s nötig sind. Weiterhin ist wichtig zu wissen, daß ein solcher Computer im Grunde nur zwei Zahlen oder Zustände kennt, nämlich 1 und 0, oder anders ausgedrückt: "Strom-da" und "Strom-nicht-da".
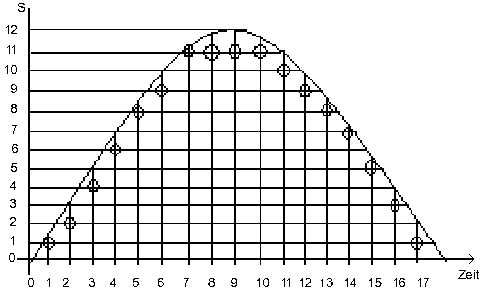
Also wird klar, daß im Digitalen Bereich eine Schaltung, wie wir sie bis jetzt im analogen Bereich kennengelernt haben, nicht mehr existiert - sie wird gerechnet, also simuliert. Dazu muß ein Signal in einzelne Segmente zerlegt werden. Dazu braucht ein Rechner oder Baustein eine gewisse Zeit. Gehen wir hier davon aus, daß er zur Verarbeitung eines einzelnen Signalsegmentes 1 ms benötigt. Wie sieht nun der Computer unser Sprachsignal?

Hier sieht man die schematische Darstellung, wie digital ein Signal in Segmente zerlegt wird. Wenn man jetzt die Werte der X-Achse (Zeit in mS) entsprechend abliest, erhält man folgende Wertetabelle (Werte der X-Achse in oberer Reihe) :
&xnbsp;
|
ms |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
&xnbsp; |
0 |
1 |
2 |
4 |
6 |
8 |
9 |
11 |
11 |
11 |
10 |
10 |
9 |
8 |
7 |
5 |
3 |
1 |
&xnbsp;
Die Abtastfrequenz 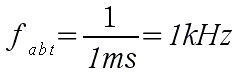
&xnbsp;
Um ein Signal digital weiterzuleiten, muß es natürlich aus dem analogen Bereich (Sprache) in den digitalen Bereich (Zahlen) umgewandelt werden. Gleiches gilt für die Empfängerseite, bevor ein digitales Signal wieder analog als Sprache im Lautsprecher zu hören ist. Für diese Umwandlung benutz man einen sog. Digitalen Signalprozessor (DSP). Er ist im Prinzip recht einfach aufgebaut und besteht aus zwei Wandlern und einem Computer (IC).
&xnbsp;
Schematische Zeichnung eines DSP

A/D-Wandler (Analog-Digital-Wandler) wandeln ein analoges Signal in digitale Werte um, D/A-Wandler machen genau das Gegenteil. So wird ein Signal digital verarbeitet.
Welche Auswirkung hat nun die Signalaufbereitung durch den DSP auf unser Signal bzw. Spektrum ? Welche Vorteile hat die digitale Signalverarbeitung neben der Platzersparnis?
Schauen wir noch einmal auf die Grafik unseres Ausgangssignals und dessen Spektrum:
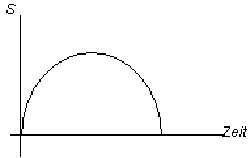
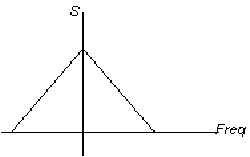
Ausgangssignal Spektrum
Der D/A-Wandler, der das digitale Signal wieder umwandeln muß, übernimmt jetzt einfach die digital vorliegenden Werte aus der Tabelle (s. Seite 27) und generiert daraus die nötigen analogen Spannungssegmente.
Wenn man genau hinsieht bemerkt man, dass die digitalen Werte anscheinend nicht den gesamten vollständigen Umfang des Spektrums wiedergeben. Dies ist auch korrekt. Ein nicht aufbereitetes, D/A-gewandeltes Signal hätte immer ein leichtes Hintergrundrauschen. Dieses Rauschen wird einfach bei der Wiedergabe rausgefiltert.
&xnbsp;
Wie man sieht, kommt es also hier auf die Abtastfrequenz an. Ist sie zu niedrig, geht zuviel Information verloren. Hier läßt sich auch eine Regel aufstellen:
Die Abtastfrequenz fabt muß größer/gleich 2 x fgesamt sein (Nyquist-Kriterium)
&xnbsp;
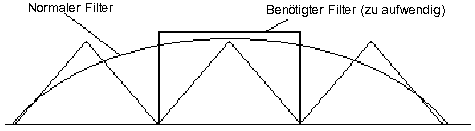
Da die Spektren direkt nebeneinander liegen, müssen wir uns einen passenden Filter aussuchen, um das gewünschte Signal zu erhalten. Schauen wir uns an, wie ein normaler Filter arbeiten würde:
&xnbsp;
&xnbsp;
Es wird klar, daß der normale Filter, der auch kostengünstig wäre, nicht in der Lage ist, unser Signal wie gewünscht zu filtern. Der dazu benötigte, sehr steilflankige Filter wäre sehr aufwendig und teuer. Also muß man einen Weg finden, einen normalen Filter einsetzen zu können. Dies erreicht man mit einem Trick, dem sog. Oversampling. Man läßt dabei den Computer Zwischenwerte errechnen und tut so, als sei die Abtastrate höher als sie tatsächlich ist. Dabei werden Änderungswerte am Original berechnet, die diesem quasi entsprechen. Dadurch "rutschen" die Spektren weiter auseinander, wodurch nun ein normaler Filter verwendet werden kann.
&xnbsp;
Grafisch dargestellt sähe das dann so aus:

Wir unterscheiden also im Grunde 4 Signalgruppen:
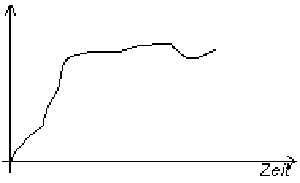
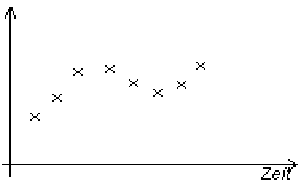
Analog = wertkontinuierlich Digital = zeitdiskret
= zeitkontinuierlich = wertdiskret
&xnbsp;
&xnbsp;

abgetastete Signale Quantisierte Signale sind zeitdiskret und sind zeitkontinuierlich wertkontinuierlich und wertdiskret
&xnbsp;
Das binäre Zahlensystem, bestehend aus den Zahlen 0 und 1, ist die interne "Computersprache". Wie stellt man mit zwei Zahlen nun verschiedene Buchstaben und Zahlen dar. Dazu nur eine kleine Tabelle:
&xnbsp;
Dez Binär
|
0 |
0 |
|
1 |
1 |
|
2 |
10 |
|
3 |
11 |
|
4 |
100 |
|
5 |
101 |
|
6 |
110 |
|
7 |
111 |
&xnbsp;
Die einfachste digitale Betriebsart im Funk ist Packet-Radio. Zur Übermittlung von Daten reichen also zwei Zahlen bzw. Töne für zwei Zustände aus.
Ein solches Übertragungsverfahren mit 1200 Baud hat beispielsweise die beiden Töne:
1,2 kHz für den Wert 0 und 2,2 kHz für den Wert 1
Dieses Verfahren nennt man AFSK (Audio Frequence Shift Keying).
&xnbsp;
Welche Bandbreite hat nun ein so erzeugtes Signal. Dazu müssen wir 2 mal die maximale Frequenz plus dem Frequenzhub von 3 kHz in folgende Formel bringen, um die Bandbreite Delta f für 1200 Baud AFSK zu berechnen:
![]()
&xnbsp;
Dies ist ein relativ breites Spektrum, da ich ja modulieren muß. Nun gibt es einen Trick, wie man die Bandbreite reduzieren kann. Dazu wird der Träger selbst (HF) verschoben. Als Beispiel nehmen wir einen Träger + 5kHz = 1 und Träger - 5kHz = 0
![]()
&xnbsp;
Diese Bandbreite ist allerdings nicht akzeptabel. Daher wurden Decoder entwickelt, die nicht mit 5 sondern 3 kHz arbeiten, so daß heute folgende Bandbreite erreicht wird:
![]()