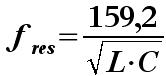
Zum Handwerkszeug des Funkamateurs gehört auch die Mathematik. Wie will ich eine Schaltung berechnen, wenn ich mit einer Formel nichts anzufangen weiss? Also - hier einige Anleitungen zu Formeln und dem Umstellen von Formeln.
Unter dem Begriff umstellen versteht man in der Mathematik die Transformation von Formeln. Dabei muss die Wertigkeit einer Formel immer erhalten bleiben. Erinnern Sie sich daran, dass eine Formel aus einem Ausdruck besteht, der z.B. zwei Ausdrücke durch ein Gleichheitszeichen verbindet:
a = 1 . b
Die Variable a ist gleich der Multiplikation von 1 mal b. Hier ist leicht zu erkennen, dass b dann benauso gross (oder klein) wie a sein muss, ansonsten würde diese Bedingung nicht stimmen. Wenn man es mit absoluten Zahlen ausdrückt und für die Variable a einen Wert von 5 annimmt, würde die Formel lauten:
5 = 1 . b
Wenn 5 = 1 . b ist, dann muss also laut Formel 1 . b auch gleich 5 sein. Somit muss b = 5 sein, damit die Bedingung stimmt (5 = 1 . 5)
In diesem einfachen Beispiel erkennt man schon auf Anhieb, wie gross b sein muss. Bei komplexeren Formeln geht das nicht. Diese muss man dann umstellen, um korrekte Ergebnisse zu erhalten.
Beispiel: a = 2 . b
Wir werden jetzt diese einfache Formel a = 2 . b nach b umstellen - denn wir wollen
eine Aussage haben, wie gross b ist. Anders gesagt: b soll alleine auf einer Seite des Gleichheitszeichens
stehen bleiben.
Dabei gehen wir davon aus, dass
kein Wert bekannt ist. Durch das Umstellen vereinfachen wir die Formel so, dass eine für uns nachvollziehbare
bzw. berechenbare Aussage entsteht. Das funktioniert wie folgt.
Um die Wertigkeit einer Formel unbedingt aufrecht zu erhalten, muss man grundsätzlich alle Operationen, die man auf einer Seite des Gleichheitszeichens tätigt, auch auf der anderen Seite durchführen. Unsere Beispielformel hat links vom Gleichheitszeichen "a" stehen und rechts davon " 2 . b "
Ich stelle jetzt die Formel um, indem ich durch 2 dividiere - auf beiden Seiten der Formel:
a = 2 x b 2 2
Dem Geübten springt sofort ins Auge, dass sich auf der rechten Seite 2 : 2 aufhebt, also weggekürzt werden kann, weil 2 : 2 = 1 ist, somit 1 x b übrigbleibt, also nur b. Die Formel lautet nun:
a = b 2
Wir haben unser Ziel erreicht: b steht alleine auf einer Seite der Formel. Nun haben wir auch eine eindeutige Aussage über den Wert von b - er ist so gross wie die Hälfte von a.
Hinweis: Das Umstellen von Formeln ist Alltagswerkzeug für den Funkamateur. Daher muss es jeder beherrschen. Wer die Unterstufenmathematik (Bruchrechnen, Prozentrechen etc) nicht beherrscht, muss dies nachholen. Dieser Stoff muss hier einfach vorausgesetzt werden.
Übung
Das Formelumstellen ist eine Sache, die man unbedingt beherrschen muss. Man ist dann in der Lage, aus einer bekannten Formel andere ("unbekannte") Formeln zu entwickeln, sprich abzuleiten. Man kann die Formeln natürlich auch auswendig lernen, aber erstens sind es ziemlich viele und - wenn man das Umstellen beherrscht, geht es meistens viel schneller. Schauen wir uns dazu noch einmal unsere Formel für die Resonanzfrequenz an und stellen sie einmal um.
Die Formel für die Resonanzfrequenz lautete in der vereinfachten Form:
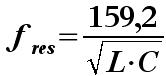
&xnbsp;
Wir wollen nun aus dieser Formel heraus wissen, wie sich L berechnet. Dazu müssen wir die Formel so umstellen, daß nur noch L auf einer Seite vom Gleichheitszeichen steht.
Umstellen bedeutet ja, daß Operationen durchgeführt werden müssen, die den von uns gewünschten Wert (hier L) isolieren. Hierbei ist aber sehr wichtig:
Merke : Beim Umstellen von Formeln angewandte Rechenoperationen müssen
immer auf beiden Seiten des Gleichheitszeichens getätigt werden.
Oder anders gesagt: Was ich links vom Gleichheitszeichen mache, muss ich auch rechts machen.
Wichtige Grundregeln
Dazu muß man auch wissen, daß sich z.B.
- Addition durch Subtraktion (und umgekehrt)
- eine Division durch eine Multiplikation (und umgekehrt)
- eine Quadratur durch eine Wurzel (und umgekehrt)
aufheben läßt.
In unserem Fall müssen wir die Wurzel unter dem Bruchstrich auflösen. Dazu müssen wir auf beiden
Seiten also zunächst quadrieren:
&xnbsp;
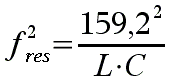
Links steht nun f 2 anstatt f und auf der rechten Seite haben wir jeweils Zähler und Nenner des Bruches quadriert. Dadurch fällt im Nenner die Wurzel weg.
Nun müssen wir den nächsten Umstellungsschritt tun, um L weiter zu isolieren. Die Division durch L (im Nenner steht ja noch LxC) hebt sich auf durch Multiplikation mit L, also auf beiden Seiten mit L mulitplizieren:
&xnbsp;
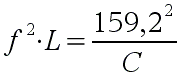
Jetzt habe ich L schon fast ganz isoliert. Die Multiplikation hebt sich auf durch Division, hier also muss ich durch f 2 dividieren, natürlich auf beiden Seiten:
&xnbsp;
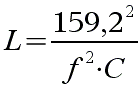
Damit habe ich L alleine isoliert und könnte mit dieser Formel schon L ausrechnen, wenn ich die Werte für f&xnbsp;und C kennen würde.
Wenn wir nun die Formel auch nach C umstellen, dann haben wir bereits drei Formeln, mit denen wir arbeiten können:
&xnbsp;
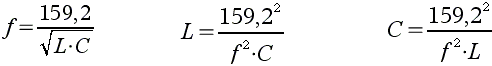
&xnbsp;
Wer diese "Umstellerei" der Formeln nicht beherrscht oder das Prinzip noch nicht begriffen hat, der möge sich den Exkurs antun. Das PDF kann auch durch Rechtsklick mit der Maus auf diesen Link runtergeladen werden.